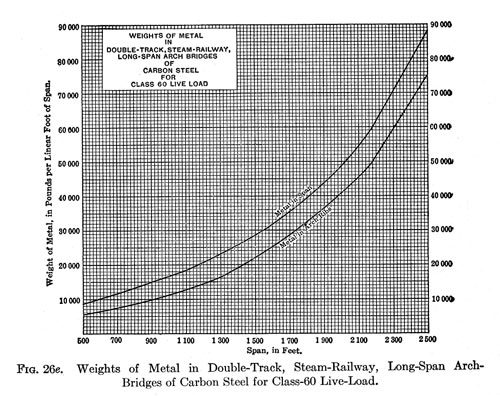
This is the theoretical limiting span-length for three-hinged arches of carbon steel, or the span at which such an arch could carry nothing but its own weight without being over-stressed. It will be noted that this limiting length is the reciprocal of the dead-load coefficient in Equation (4), and that a vertical line on the diagram of arch-rib weights per lineal foot of span, drawn through the abscissa point which represents this value of l, will be asymptotic to the weight curve.

Fifth. From the curves in the diagrams it is possible to determine the economic or practicable limit of arch spans, by assuming, as the author did years ago in his economic investigations for cantilevers, that the said

magnify image

limit is reached when it takes 4 1/2 lbs. of metal to carry 1 lb. of live load. On that basis, and assuming that the equivalent uniform live load per lineal foot for a long span is equal to the car load per lineal foot, the limiting weight of metal per foot for carbon-steel, double-track, steam-railway bridges of Class 60 would be 4.5 X 12,000 = 54,000 lbs. Referring to Fig. 26e, it is found that the span for that weight is nearly 2,100 ft.; consequently, generally speaking, it may be stated that, for steam-railway arch-bridges of carbon steel, the limiting length of span is about 2,000 ft., or the same as the limiting length of main opening in cantilever bridges built of the same material. Judging by analogy, the corresponding practicable limiting length of nickel-steel arch-spans is about 2,600 ft.

Sixth. It is impracticable to take the substructure into account when