| 178 | ECONOMICS OF BRIDGEWORK | Chapter XX |
|
Therefore the total weight of girder will be
Differentiating with respect to h and placing the differential coefficient
Hence
from which we find
and
But the value of c is generally about 0.3. Substituting this gives
But the first member of this equation represents the weight of the flanges for the most economic condition, and the second member is eighty-four per cent of the total weight of the web plate without its details. Dividing both sides of the last equation by 0.8 and canceling the 3.4 l
or
Evidently the first member of this equation represents the gross area of the flanges and the second member differs only a little from the gross area of the web and may without any great error be called such. Hence it may be stated that the theoretical maximum of economy exists when the gross areas of flanges and of web at mid-span are equal-a condition readily remembered. If the depth of web be selected on this basis, rather than by the old criterion which makes the total weight of flanges equal to the total weight of web with all its details, it will be found to give a greater web depth. This increased depth is likely to augment the cost from one or more of the following practical considerations which the formula cannot take into account: |
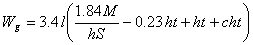
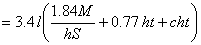 [Eq. 7]
[Eq. 7]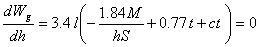 [Eq. 8]
[Eq. 8]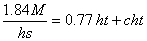 [Eq. 9]
[Eq. 9]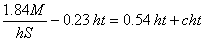 [Eq. 10]
[Eq. 10]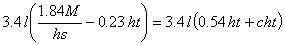 [Eq. 11]
[Eq. 11]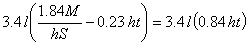 [Eq. 12]
[Eq. 12]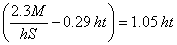 [Eq. 13]
[Eq. 13]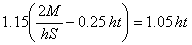 [Eq. 14]
[Eq. 14]