| 176 | ECONOMICS OF BRIDGEWORK | Chapter XX |
|
If C is to be made a minimum, we shall have, by differentiation, |
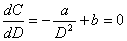 | [Eq. 2] |
|
or |
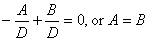 | [Eq. 3] |
|
As the second differential coefficient, after substitution according to the usual method of maxima and minima, comes out positive, the result obtained corresponds to a minimum. From this it is evident that, for trusses with parallel chords, the greatest economy of material will prevail when the weight of the chords is equal to the weight of the web. The author has verified this conclusion by checking the weights of chords and webs in a number of finished designs, finding it to be absolutely reliable. However, it is not of much practical value, because the economic depths of trusses with parallel chords are pretty well known; and, again, when spans are in excess of 175 or 200 feet, the chords of through-bridges are seldom made parallel. Moreover, the best depth to use is not often the one which gives the least weight of metal in the trusses. It has been found by experience that, for trusses with polygonal top chords, the economic depths, as far as weight of metal is concerned, are generally much greater than certain important conditions will permit to be used. For instance, especially in single-track, pin-connected bridges, after a certain truss depth is exceeded, the overturning effect of the wind-pressure is so great as to reduce the dead-load tension on the windward bottom chord to such an extent that the compression from the wind load carried by the lower lateral system causes reversion of stress, and such reversion eye-bars are not adapted to withstand. A very deep truss requires an expensive traveler, and decreasing the theoretically economic depth increases the weight but slightly; hence it is really economical to reduce the depth of both truss and traveler. Again, the total cost of a structure does not vary directly as the total weight of metal, for the reason that an increase in the sectional area of a piece adds nothing to the cost of its manufacture, and but little to the cost of erection; consequently it is only for raw material and freight that the expense is really augmented. Hence it is generally best to use truss depths considerably less than those which would require the minimum amount of metal. For parallel chords, the theoretically economic truss-depths vary from one-fifth of the span for spans of 100 feet to about one-sixth of the span for spans of 200 feet; but for modern single-track-railway through-bridges the least allowable truss- depth is about 30 feet, unless suspended floor-beams be used, a detail which very properly has gone out of fashion. In two five-hundred-foot spans of a combined railway and highway bridge the author employed a truss depth of seventy-two feet; but, this was determined by the reversal of stress in bottom chords through wind- |