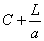In comparing the economics of several methods of accomplishing the same result, the author has advocated the method of computing and contrasting the total annual costs, including interest on first cost, upon the assumption that all the money needed for the construction had been borrowed; and this is the most logical method, although in his practice he has sometimes adopted other methods—mainly to please his clients. Some clients want to see figures of total cost instead of estimates of annual expense; and, under such a condition, it is necessary to sum up for each case all annual expenses except interest, ascertain what amount of money would produce this sum by simple interest at current rates; and add that amount to the total first cost. The case giving the least grand total would be the economic one.

An effective method of contrasting several differing types of construction for their economics is that used in Case III, viz., to assume a number of future dates, preferably those at which certain large expenditures would probably have to be made for renewals or repairs of perishable portions, and compute the grand total cost to each date for each proposed structure under the assumption that it is then put into perfect condition, and allowing standard compound interest not only on the first cost but also on all annual expenditures. A comparison of these grand total costs at the several dates adopted will indicate clearly which is the most economic of all the types of construction compared.

To those who have a penchant for using mathematical formulae, the following economic treatment will appeal. It was evolved some forty years ago by Ashbel Welsh, past-president of the American Society of Civil Engineers.

TO FIND THE COMPARATIVE ECONOMY OF TWO BRIDGES OF DIFFERENT COST AND

DURABILITY, THAT WILL ANSWER THE SAME PURPOSE EQUALLY WELL WHILE

THEY LAST

"Let C be the cost and assumed real value of one of them, T the time it will last, a the compound interest on one dollar for that time, at whatever rate money is worth to the party paying for the bridge, and L the loss on the bridge at the end of the time T, or the amount which it would take to make it as good as new. Let R be the real value of the other bridge, C' its cost, T' its duration, a' the compound interest on one dollar for that time, and L' the loss on the bridge at the end of the time T', or the amount required to make it as good as new. And let V be the real value of the bridge that would last forever, if all circumstances should remain constant.

"Now, supposing that the money required for building had been borrowed for an indefinite time, the actual expense at the end of the time T to the party paying for the bridge which would last forever would be a V; and the actual expense at the end of the same time for the first bridge, after making it as good as new, would be a C + L. These two quantities are equal: therefore the hitherto unknown value of V is

"Similarly, at the end of the time T', the expense for the bridge which would last forever would be a' V; and that for the second bridge, after making it as good as new,