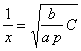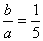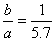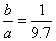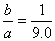in which y (the total cost of bridge) is a minimum when

where      A = cost of two end abutments in dollars;

B = cost of the floor and that part of the metal weight

which remains constant, in dollars;

C = cost of one pier in dollars, assumed as constant;

l = length of bridge in feet;

x = number of spans;

p = price of metal per pound, in dollars;

y = total cost of bridge in dollars;

and         a = weight per foot of a span b feet in length.

Thus far all right; but then he makes an assumption which will not be correct except for one live load, for one set of specifications, and for single-track railway bridges, viz., that for pin-connected spans

On account of this assumption his subsequent table of economic span lengths is not in any sense general, but is true only for single-track bridges designed for one standard live load and according to one standard set of specifications; while his equations hold good for bridges of any kind and loading, including highway as well as railway structures.

As a check on the correctness of Mr. Bryan's assumption that

for single-track bridges, the author has looked up some of his designs and has found the following: For a 375-ft. through-span, Class X,

for a 362-ft. double-track through-span, Class Z,

and for a similar 490-ft. span,

For a 280-ft. double-track deck-span,