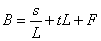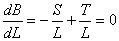The cost per foot of the floor system is practically independent of the span length, being a function of the panel length, which does not change materially with the span. We now have the equation

In which B is to be made a minimum.

Differentiating, we have (as F is a constant)

or    S = T

A further differentiation shows that the result corresponds to a minimum.

In reality the truss weight per foot increases more rapidly than the span length. If r is the ratio of span lengths, the truss weights, for small changes in span lengths, will vary almost exactly according to the ratio. On the other hand, the weight per foot for the lateral system does not increase as rapidly as the span, unless the perpendicular distance between central planes of trusses also increases. Unfortunately, though, the gain in truss weight over that given by the assumed theory of variation is generally greater than the corresponding loss for the weight of lateral system. consequently the combined weights per foot of trusses and laterals generally increase a trifle faster than the span length. This is partially offset by the fact that the pound price of metal erected and painted will reduce a trifle as the weight per foot increases.

Again, there is sometimes a small error in the assumption that the cost of the piers varies inversely as the span length, because the size of each pier may have to be increased a little to accommodate the heavier spans. If the perpendicular distance between central planes of trusses is increased because of the greater span length, the cost of each pier will be increased because of its greater length; but this will occur only occasionally.